03 Jul Do Yawl do Petri Nets
Where do you draw a line?
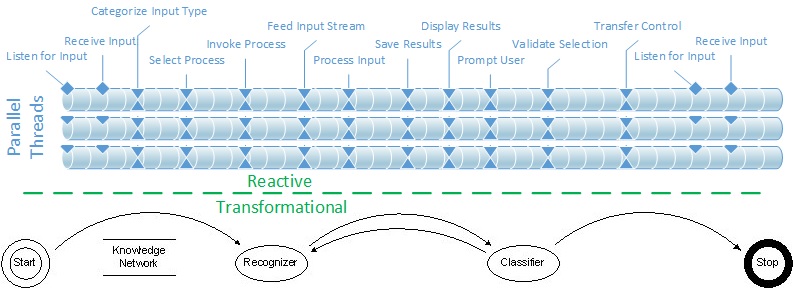
In geometry, digital theory, language and time, patterns tend to be linear: they bear distinct sequences. The sequences in these domains either contribute to the meaningfulness of the patterns, or, in the case of time, are the foundation of the patterns. Any logic that focuses on these sequential patterns is linear logic. Temporal Logic (TL) is a convenient linear formalism for specifying and verifying properties of reactive systems over time. Reactive systems, such as web portals and device operating systems, can run for an indeterminate amount of time, taking inputs from a variety of sources and delivering outputs on a recurring or continual basis. The upper part of this illustration shows how reactive systems might be designed to run cyclically without stopping.
Transformational systems, on the other hand, take an input at the beginning, progress through a set of states, deliver a result, then end or start over again. Bulk data transfers and income tax calculators are typical examples. State diagrams are usually good for describing transformational systems. Reactive systems are better described using Temporal Logic as illustrated in the multi-threaded example above. Petri nets are state diagrams with tighter design constraints, but similar interpretation. “The graphical nature of Petri nets, their explicit representation of the notion of state, and the existence of analysis techniques made them eminently suitable for workflow specification” (W van der Aalst in ter Hofstede 2010 p.10). Add a “Start” point and an “End” point and it becomes a “workflow net”.
| Understanding Context Cross-Reference |
|---|
| Click on these Links to other posts and glossary/bibliography references |
|
|
|
| Prior Post | Next Post |
| SPARQL Fireworks | |
Definitions |
References |
| Aceto 2007 ter Hofstede 2010 | |
| Kansas State LTL Patterns | |
| YAWL |
The modalities in Temporal Logic are time-dependent abstractions of activities, changes or time-dependent facts, along the linear axis of time: past, present and future. In my experience, the best way to 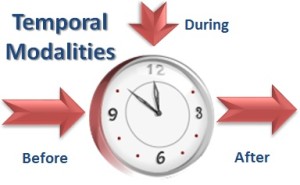 represent temporal logic provides both a reference point in the past, present or future, and a direction if applicable. Sometimes we can’t know, in advance, the actual day and hour of the reference time, or we are discussing fictional time (such as after Bilbo confronted Smaug and before Frodo left the Shire). I’ve provided a table with some examples of modalities that include both a reference point and a direction (see the illustration for arrows representing “direction”):
represent temporal logic provides both a reference point in the past, present or future, and a direction if applicable. Sometimes we can’t know, in advance, the actual day and hour of the reference time, or we are discussing fictional time (such as after Bilbo confronted Smaug and before Frodo left the Shire). I’ve provided a table with some examples of modalities that include both a reference point and a direction (see the illustration for arrows representing “direction”):
| Reference | Prior Mode | Concurrent Mode | Post Mode |
| Point in the Past | until | during | after |
| The Present | until | during | after |
| Point in the Future | until | during | after |
| Unknown Future Time | until | during | after |
| Unknown Past Time | until | during | after |
| Fictional Time | until | during | after |
The referenced point in time may be measured as a discreet mark such as a millisecond for dense activities such as CPU computation cycles, or a specific time on a specific date. The reference point may, instead, be a time segment as few as a defined number of milliseconds or entire epochs lasting arbitrary numbers of years or millennia. For any phenomenon that is time-bound, an accurate TL formula can be articulated that places the phenomenon in context. Other modalities could include “long before” or “long after”, and the useful list of modalities is much larger.
Workflow systems that use steps and branches are straightforward implementations of linear logic engines. I speak of the power of workflow in my Hobbit post. Linear Temporal Logic may be a valuable tool in your belt if you know the sequence of tasks or activities that need to take place in your system to produce the needed outcome. If you don’t know the sequence, goal-oriented or backward chaining logic may be needed.
YAWL is Yet Another Workflow Language. They describe their tools as: “YAWL is a BPM/Workflow system, based on a concise and powerful modeling language, that handles complex data transformations, and full integration with organizational resources and external Web Services.” YAWL can be used to implement linear temporal logic with the important distinguishing feature that it can enforce the restrictions defined in Petri Nets (arcs must span different node types – never the same).
Petri Nets and Linear Temporal Logic.
 A Petri net is a directed bipartite graph, in which the event nodes or vertices represent transitions (i.e. events that may occur, signified by bars) and states or places (i.e. conditions, signified by circles). The directed arcs or edges describe which places are pre- and/or post-conditions for which transitions (signified by arrows). Some sources[1] state that Petri nets were invented in August 1939 by Carl Adam Petri — at the age of 13 — for the purpose of describing chemical processes. A Petri net consists of places, transitions, and arcs. Arcs run from a place to a transition or vice versa, never between places or between transitions. The places from which an arc runs to a transition are called the input places of the transition; the places to which arcs run from a transition are called the output places of the transition (see W van der Aalst in ter Hofstede 2010 p.10). YAWL and other workflow engines provide formalized mechanisms for creating Petri Net based workflows.
A Petri net is a directed bipartite graph, in which the event nodes or vertices represent transitions (i.e. events that may occur, signified by bars) and states or places (i.e. conditions, signified by circles). The directed arcs or edges describe which places are pre- and/or post-conditions for which transitions (signified by arrows). Some sources[1] state that Petri nets were invented in August 1939 by Carl Adam Petri — at the age of 13 — for the purpose of describing chemical processes. A Petri net consists of places, transitions, and arcs. Arcs run from a place to a transition or vice versa, never between places or between transitions. The places from which an arc runs to a transition are called the input places of the transition; the places to which arcs run from a transition are called the output places of the transition (see W van der Aalst in ter Hofstede 2010 p.10). YAWL and other workflow engines provide formalized mechanisms for creating Petri Net based workflows.
I suppose I’ve spent more time in this post discussing linear temporal logic than YAWL or young Mr. Petri, so I should have named it differently, but I can’t resist a play on words. You can easily implement TL in a workflow engine or a procedural coding language, and you cannot easily do so in a neural network or in LISP without contortions. There are places for LISP, or at least linked lists, and places for Neural Networks. I advocate using the right tools for the capability you’re trying to automate.
| Click below to look in each Understanding Context section |
|---|