14 Oct Knowledge in Non-Neural Models
 Non-Neural Models
Non-Neural Models
So far we have examined a number of models that are explicitly designed to be neuromorphic. This categorization is useful for two reasons:
- the apparent chaos or non-deterministic functioning of the brain is represented by these models; and
- neural networks explicitly use large numbers of distributed processors or neurodes that each contribute to the brain-like structure and functionality of the model.
If biological neurons are simple processors, not actually storing information, then implicit “connectionist” representations are naturally more neuromorphic than symbolic or explicit representation models.
| Understanding Context Cross-Reference |
|---|
| Click on these Links to other posts and glossary/bibliography references |
|
|
|
| Prior Post | Next Post |
| Neural Conceptual Dependency | |
Definitions |
References |
| Schank 1973 Sowa 1984 | |
| Schank 1986 | |
| Fensel 2004 Rish Bayesian Tutorial |
 In the next section, we will look at some other models that, instead of focusing strictly on structural neuromorphism, exhibit functionality that in some ways mirror cognitive processes, and represent knowledge in a familiar form. At the most basic level, relational databases, though bearing neither structural nor functional resemblance to the brain, bind bits of information together with explicit representations: attributes are represented as column labels in a table and associations between related concepts are linked by primary and foreign keys. There are also many systems that use forward or backward chaining inference rules. Rules, characterized by “IF” conditions or premises, and “THEN” conclusions or consequences, also represent explicit associations between things or concepts that may be treated as computational “objects.”
In the next section, we will look at some other models that, instead of focusing strictly on structural neuromorphism, exhibit functionality that in some ways mirror cognitive processes, and represent knowledge in a familiar form. At the most basic level, relational databases, though bearing neither structural nor functional resemblance to the brain, bind bits of information together with explicit representations: attributes are represented as column labels in a table and associations between related concepts are linked by primary and foreign keys. There are also many systems that use forward or backward chaining inference rules. Rules, characterized by “IF” conditions or premises, and “THEN” conclusions or consequences, also represent explicit associations between things or concepts that may be treated as computational “objects.”
The next few posts in this section will focus on models that represent associations or links between similar objects and concepts.
A New Direction
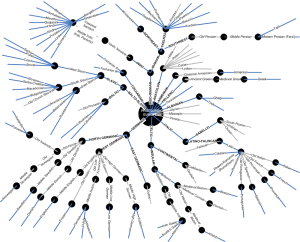
We can build multi-dimensional models for robust language understanding and translation in flat space using complex nodes and multi-directional flow. I will describe approaches for achieving this in the next few posts and later Sections. The model includes fuzzy ontologies that represent knowledge objects in context with weighted values. This illustration shows a network in which each node has an explicit value represented by one or more words. A variation on this model could represent different types of information in different formats, including nodes that may be images or sounds or aromas.
Semantic Networks
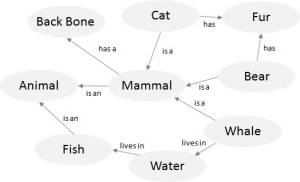 In an associationist framework, knowledge is structured as discrete elements linked by relations. The links describe how the two items are related. Modern implementations of associationist graphs are called by various names such as associative or semantic networks or conceptual graphs. Nonetheless, they tend to have the same properties. Semantic networks are simple structures based on objects linked together by a set of possible relations. These have been used persuasively to represent hierarchical relations among many objects or concepts. The simplicity arises from the fact that most semantic nets are limited to one relation between any two items. In the literature, most references to semantic networks also have a limited number of relations with which you can connect two nodes, such as “is a” and “has a” relations. The following snippet from Wikipedia shows how a semantic network may be coded:
In an associationist framework, knowledge is structured as discrete elements linked by relations. The links describe how the two items are related. Modern implementations of associationist graphs are called by various names such as associative or semantic networks or conceptual graphs. Nonetheless, they tend to have the same properties. Semantic networks are simple structures based on objects linked together by a set of possible relations. These have been used persuasively to represent hierarchical relations among many objects or concepts. The simplicity arises from the fact that most semantic nets are limited to one relation between any two items. In the literature, most references to semantic networks also have a limited number of relations with which you can connect two nodes, such as “is a” and “has a” relations. The following snippet from Wikipedia shows how a semantic network may be coded:
(defun *database* ()
– ((canary (is-a bird)
– (color yellow)
– (size small))
– (penguin (is-a bird)
– (movement swim))
– (bird (is-a vertebrate)
– (has-part wings)
– (reproduction egg-laying))))
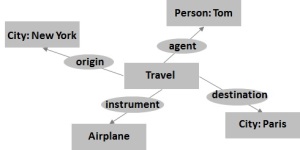 A conceptual graph permits more complex relations in structures such as type definitions. A type definition is a collection of relations that constitute a distinct phenomenon or activity. For example, a trip or travel action has an agent, an instrument or vehicle, a destination, and an origin as shown at right. Conceptual graphs may limit the number of links for each entity or the number of links between each two items. A restriction that is universal in conceptual graphs and semantic networks is that no entity will be part of the overall graph unless it has at least one connection to another entity (No Orphans Allowed). Completely unconnected groups of entities would be considered separate networks.
A conceptual graph permits more complex relations in structures such as type definitions. A type definition is a collection of relations that constitute a distinct phenomenon or activity. For example, a trip or travel action has an agent, an instrument or vehicle, a destination, and an origin as shown at right. Conceptual graphs may limit the number of links for each entity or the number of links between each two items. A restriction that is universal in conceptual graphs and semantic networks is that no entity will be part of the overall graph unless it has at least one connection to another entity (No Orphans Allowed). Completely unconnected groups of entities would be considered separate networks.
Ontologies (Fensel 2004) and Bayesian Networks (see Irina Rish’s Tutorial on Bayesian Networks) are both similar to or examples of conceptual graphs, each with different strengths. In the next two sections of this blog, I will delve further into how these non-neural models may be used to develop neuromorphic systems that can effectively perform complex brain tasks.
| Click below to look in each Understanding Context section |
|---|