08 Jan E/I Electric Potential Curve
Challenge
 I’ve noticed two phenomena in computing that have often been compared to brain activity even though they don’t significantly resemble the behavior of electrical potential changes between neurons:
I’ve noticed two phenomena in computing that have often been compared to brain activity even though they don’t significantly resemble the behavior of electrical potential changes between neurons:
- Flip-Flop (the changing of a “register” from 0 to 1
- Node Firing (The activation of a node in an artificial neural network)
In this section of Understanding Context, I’ve been trying to establish a basis for comparison between the electric potential curve experienced in the brain, and the variability in the characteristics of that curve, versus the strict inflexibility of the behavior of flip-flops and neural network nodes. The intent of this exposition is to dispel the misimpression that the behavior of artificial neural networks matches the behavior of the human neural network. Once I’ve gone through the material, it’s up to you to decide if I’m straining at gnats or if I have a valid point. Further, once I propose an alternative design, it will be up to you to decide whether I get any closer to modeling neural behavior.
| Understanding Context Cross-Reference |
|---|
| Click on these Links to other posts and glossary/bibliography references |
|
|
|
| Prior Post | Next Post |
| Excitation and Inhibition | What of Perception |
| Definitions | References |
| Flip-Flop brain | Stevens 1989 |
| Node neuron | Bingen et al 2012 Brain Geek |
| neural network modeling | Jesperson 2012 |
The Classic Curve
 Chemical reactions are very predictable because the ions in atoms are law-abiding. One of the interesting facts about chemical reactions, including those that occur at synapses in the brain, is that very small changes in the number of atoms and molecules involved can change the characteristics of the reactions. Changes in electrical potential creating impulse waves in the brain are relatively predictable, but there is variation at the microscopic level that can impact brain processes.
Chemical reactions are very predictable because the ions in atoms are law-abiding. One of the interesting facts about chemical reactions, including those that occur at synapses in the brain, is that very small changes in the number of atoms and molecules involved can change the characteristics of the reactions. Changes in electrical potential creating impulse waves in the brain are relatively predictable, but there is variation at the microscopic level that can impact brain processes.
The graph below represents changes in the electrical potential (voltage) in a typical neuron during the brief span of a spike – an excitatory action potential. The vertical axis represents electrical potential in millivolts, while the horizontal axis represents time in milliseconds. As you can see, it does not require much time or voltage to make a big difference in the flow of excitation and inhibition between neurons.
Follow the illustrated flow of an action potential impulse (or “spike” or “excitation”) over a typical few milliseconds.
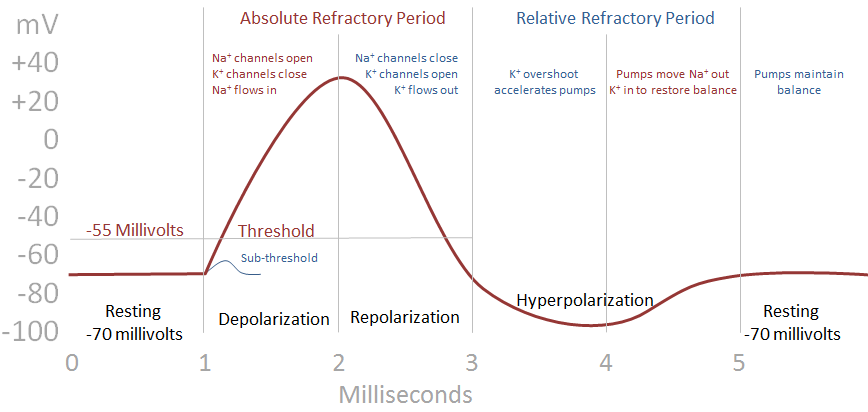 In the aftermath of a spike of excitation, the hyperpolarization process causes a refraction period at a single synapse, reducing the likelihood of proximal electrical activity creating or prolonging excitation. A neuron may, however, have multiple inputs. So the cumulative impact may be different than the local impact.
In the aftermath of a spike of excitation, the hyperpolarization process causes a refraction period at a single synapse, reducing the likelihood of proximal electrical activity creating or prolonging excitation. A neuron may, however, have multiple inputs. So the cumulative impact may be different than the local impact.
Curve Variations
 Like a symphony, action potential flow can vary. In later posts we will explore some of these variations, describe how they are caused and look briefly at the cybernetic implications. Constraints on E/I flow often change the shape of the curve. The overall intensity or amplitude of E/I impulses may depend on several factors, including the nine listed here:
Like a symphony, action potential flow can vary. In later posts we will explore some of these variations, describe how they are caused and look briefly at the cybernetic implications. Constraints on E/I flow often change the shape of the curve. The overall intensity or amplitude of E/I impulses may depend on several factors, including the nine listed here:
- the volume of neurotransmitter in the vesicles
- the volume or density of sodium, calcium and potassium
- the intensity of the impulse
- the frequency of multiple impulses
- the physical proximity of the vesicle to the synaptic channel
- the elasticity or aperture of the channel
- the number and distribution of channels in a synapse (probably consistent)
- the prior electrical potential of the cell
- the prior ionization of the fluid surrounding the synapse…
This list may be incomplete, but the moral of the story is simple: many factors influence the participation of the individual neurons and the individual synapses in cognitive processing. These factors further influence the nature of a spike, creating significant differences in their electro-chemical responses. These differences surely shape cognition in ways that we do not yet know, but can infer. I’ll save the inferences for later. For now, let’s look at the differences.
Here is a common, simple example of how not all impulses are created equal. The illustration below shows a case in which the duration of excitation (the curve is above the threshold) is twice as long as a standard spike. Depolarization acts as an inhibitor, so the sooner a neuron “settles” the less likely additional proximal electrical activity will cause the excitation to sustain. This illustration shows excitation that remains above threshold twice as long as normal.
Though secondary impulses may cross a single synapse, the chemical balance limits their frequency. A single neuron may receive input from any number of receptors. Unlike a computer, there is no clock controlling cycle speed. Differences in the behavior and shape of excitatory and inhibitory action potentials are observed in different areas of the brain, including the visual cortex, optical nerve, cerebellum and midbrain. Nerves that control muscles are particularly variable, including those mediating heart rate.
Repeated Spikes
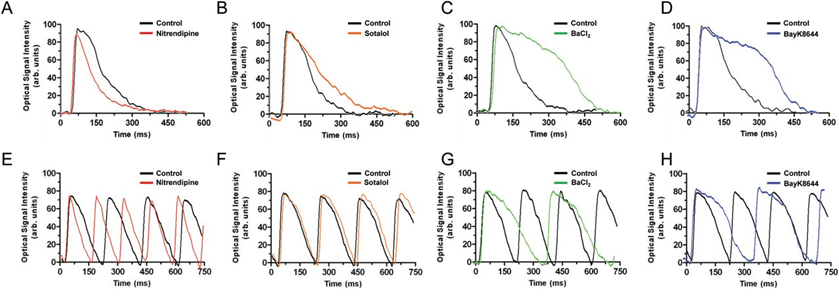
Secondary impulses can be repeated. The aggregate impact of repeated spikes may exhaust the chemical balance of the cell. Here are examples of optical neurons firing repeatedly:
These examples show potentials prolonged for hundreds of milliseconds – two orders of magnitude longer than normal spikes. We also see repeated spikes, each of longer duration. These are examples of optical signals. Cardiac muscle control neurons are often characterized by prolonged action potentials. In such a case, the pumps may have to work harder for a while to restore balance, thus causing a longer refraction period. This is another example of the variability of the action potential curve. There are more examples of variability in the patterns of electrical activity that drive our cognitive processes. This gives a flavor and a basis for developing more accurate models in computers.
| Click below to look in each Understanding Context section |
|---|




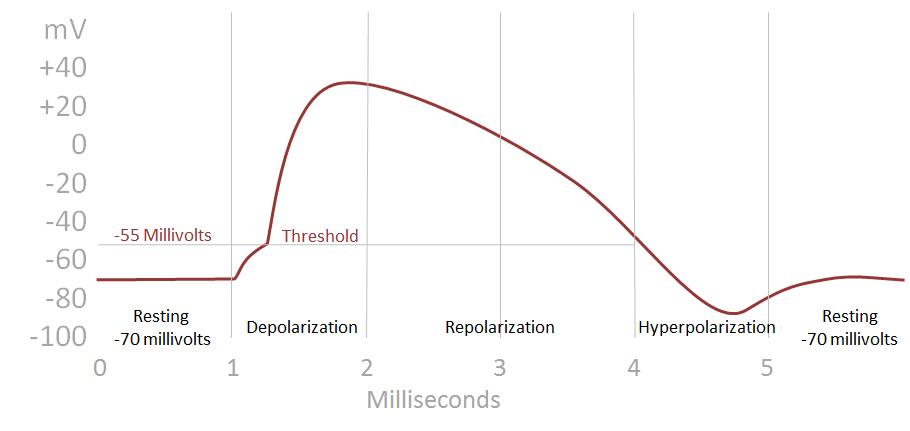




In you diagram “Follow the illustrated flow of an action potential impulse (or “spike” or “excitation”) over a typical few milliseconds.” you state that in order to abolish the negative overshoot “pumps move Na+ out and K+ in to restore the balance”. This does not make sense. The sodium/potassium pumps always move in one cycle 3 Na+ out and 2 K+ in. Therefore the overshoot should be maintained or increased by the action of the pumps, but never become more positive. Maybe you should simply consider the constant leakage of ions across the membrane instead.