31 Mar Truth, Belief and Confidence
 Establishing frameworks for truth, belief and confidence can be part of raising a child and part of building a more intelligent system. Parents in households of faith often feel a compelling need to teach their children about things that are outside the realm of scientific discovery. In espionage, intelligence analysts review information collected by agents, electronic snoops, and other sources to determine what is more credible and what is less credible. They often apply numeric credibility factors to information.
Establishing frameworks for truth, belief and confidence can be part of raising a child and part of building a more intelligent system. Parents in households of faith often feel a compelling need to teach their children about things that are outside the realm of scientific discovery. In espionage, intelligence analysts review information collected by agents, electronic snoops, and other sources to determine what is more credible and what is less credible. They often apply numeric credibility factors to information.
For an automated system whose sole purpose is to understand the intent of a human speaker, value judgments about truth and accuracy are secondary. The real question for the system is: “To what level of confidence can I (me being the system) aver that I understand your (the human speaker’s) intent?” To even be able to track the possible answers to this question, a system will need to process things in the context of multivalued logic.
| Understanding Context Cross-Reference |
|---|
| Click on these Links to other posts and glossary/bibliography references |
|
|
|
| Prior Post | Next Post |
| Is Anything True or False | Generating and Qualifying Propositions |
| Definitions | References |
| truth belief confidence | Davidson 2003 |
| intelligence multivalued logic | Nguyen 2006 |
| fuzzy inference | Stanford Plato on Fuzzy Logic |
 An instructive example of multivalued logic is the confidence we place in the things we hear and read. We often describe the confidence we feel in fuzzy terms, such as “fairly” confident and “not very” confident. The things we see, such as the fur on a little animal, can be “understood” with high confidence. The swirling, dance-like motion of a flock of migrating birds settling into a tree may be more wondrous and difficult to analyze.
An instructive example of multivalued logic is the confidence we place in the things we hear and read. We often describe the confidence we feel in fuzzy terms, such as “fairly” confident and “not very” confident. The things we see, such as the fur on a little animal, can be “understood” with high confidence. The swirling, dance-like motion of a flock of migrating birds settling into a tree may be more wondrous and difficult to analyze.
In artificial intelligence systems that employ fuzzy techniques, truth values or confidence values are often applied to the rules or data used in inference and/or to the conclusions generated by the system. Confidence values can be used in the inference process to select among multiple possible decisions or solutions. A confidence value applied to a single solution can provide the user with a gauge to determine how much trust to place in the solution. An answer near or beyond the boundaries of a system’s knowledge would naturally get a lower confidence value than an answer that the system was able to generate through a straightforward process with little or no ambiguity.
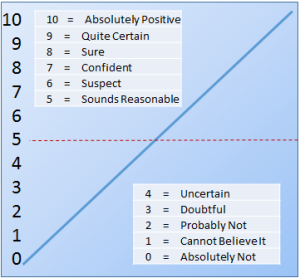 We reason about the world with more or less confidence, depending on how concrete the proposition appears. This type of scaled reasoning process, where we trust in perceived things more than hearsay or reported things, can be described in terms of a continuum with numbers marking points in the line. We might use a numerical version of multivalued logic to represent confidence values as shown in the illustration at right. By the numbers, a perfect 10 represents absolutely positive. But one person’s certainty of a thing does not make it true. Again, when working toward intent, we’re less concerned about truth, per se, and more about confidence.
We reason about the world with more or less confidence, depending on how concrete the proposition appears. This type of scaled reasoning process, where we trust in perceived things more than hearsay or reported things, can be described in terms of a continuum with numbers marking points in the line. We might use a numerical version of multivalued logic to represent confidence values as shown in the illustration at right. By the numbers, a perfect 10 represents absolutely positive. But one person’s certainty of a thing does not make it true. Again, when working toward intent, we’re less concerned about truth, per se, and more about confidence.
Types of Propositions
How can common sense knowledge be expressed in terms a computer might understand? To answer that question, we must once again consider the concept of propositions. Communication is our means of expressing and sharing propositions. Since communication is the subject of Volume 6, this section will focus on work done by psychologists and others in determining and modeling common sense reasoning.
Common sense knowledge fits into the basic or simple end of the proposition spectrum. Reasoning complexity may be describable on a scale of activation in the brain. Simple propositions are likely to highly activate fewer neurons than complex ones. The subjective words in the illustration represent this scale of activation.
Ascriptive propositions are existential: they ascribe attributes to things, including the class to which they belong. Is there a dichotomy between complex causal propositions that involve, to some extent, deep reasoning, and ascriptive propositions involving common sense? Much of common sense involves causal propositions learned from observation. Ascriptive propositions can be simpler because they are directly tied to perception, and seeing is believing.
Propositions as Associations
 Propositional logic can fit into an associationist model. If a proposition is a basic component of thought, what does it embody? A proposition might say that the attribute of having FUR can correctly be generalized for LITTLE ANIMALS. This proposition may then be stated in a more formulaic manner by applying the ascriptive relation “HAS” to members of the class of real objects named LITTLE ANIMAL. Using a general formula template
Propositional logic can fit into an associationist model. If a proposition is a basic component of thought, what does it embody? A proposition might say that the attribute of having FUR can correctly be generalized for LITTLE ANIMALS. This proposition may then be stated in a more formulaic manner by applying the ascriptive relation “HAS” to members of the class of real objects named LITTLE ANIMAL. Using a general formula template
OBJECT RELATION OBJECT,
the proposition may be stated:
LITTLE ANIMAL HAS FUR.
Establishing ascriptive relations such as color, shape, relative size, and the like, are perceptually oriented and require minimal or no reasoning. Much of common sense reasoning is based on simple attributes of objects. Relative size is a clear example. We can imagine an elephant hurting a mouse but not vice versa. We can envision a forest burning but not a lake or an ocean, but when we see fire on water once, it becomes much more logical the next time we see it. Seeing is believing, though not necessarily understanding. Ascriptive relations describing attributes of the objects in question give us clues on which we base expectations that help us interpret things we see.
In our model, different kinds of relations between associated objects play key roles.
| Click below to look in each Understanding Context section |
|---|
| Intro | Context | 1 | Brains | 2 | Neurons | 3 | Neural Networks |
| 4 | Perception and Cognition | 5 | Fuzzy Logic | 6 | Language and Dialog | 7 | Cybernetic Models |
| 8 | Apps and Processes | 9 | The End of Code | 10 | Glossary | 11 | Bibliography |