17 Oct Neural Conceptual Dependency
 Conceptual Dependency
Conceptual Dependency
Much of this blog has been about knowledge representation: how the brain might learn and process it, how cognitive functions treat knowledge, and now, how computers may store and process it. Conceptual structures and conceptual dependency theories for computation have been useful for categorizing and representing knowledge in intuitively simple and cognitively consistent schemata (Sowa 84). The computational perspective of these representations is straightforward:
- data items are linked by address or index; and
- specific relations may be attached to links.
In my prior post on Knowledge in Non-Neural Models, I showed how these linkages may be created in semantic networks or concept graphs. If data are in expandable, indexed files, and the files are cross indexed, as is being done commonly now using NoSQL, a potentially limitless graph can be created. Because infinite structures are difficult to create and manage, however, limits can be imposed on the number of files in the conceptual graph and the number of indices in each file. The more knowledge management is automated with intelligent rules, and checks and balances, the higher the limit can be. If the arbitrary limit is high enough, 5 assume that a knowledge base could contain as much data as the human brain, or for that matter, if it is very well organized, all the accumulated knowledge of humanity. Though its internal structure may be optimized for the hardware and software of the intelligent system it serves, a concept graph can be externally represented as an associationist network of entities and links.
| Understanding Context Cross-Reference |
|---|
| Click on these Links to other posts and glossary/bibliography references |
|
|
|
| Prior Post | Next Post |
| Context Powers Backward Chaining Logic | |
Definitions |
References |
| Schank 1976 Sowa 1984 | |
| McCreary 2014 | |
| Selfridge 1958 Scott 1976 |
In semantic networks and concept graphs, links within the specific areas, or knowledge domains of the network, and to peripheral processing centers may be simple or complex. As described in the prior post, a simple link could just connect two labeled items, or it may have an “is a” or “has a” label. A complex link would connect two labeled items with a link that can contain complex causal, constructive, commercial, identity, or other named relationships. Rules in such a system may act on the named nodes, the named relations, or, most effectively, a combination of both.
How complex links might be formed in the brain is still a matter of speculation. Perhaps the associated item and the relationship between the two items are linked to the original item by cooperative synaptic links. It is possible, though less likely, that relationship data may be explicitly stored in filaments in the dendrites connecting the associated knowledge loci.
 Conceptual Model Adaptability
Conceptual Model Adaptability
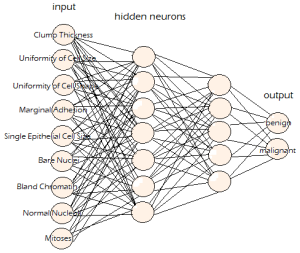
In the neural network models like those described in this Section, nodes are shown as circles, and links are shown as lines connecting the circles. In the networks depicted as non-neural models, the links are not just lines, but labeled lines. The labels identify the relation that connects the two entities. In some neural networks, it is difficult, if not impossible, to implement intelligent links. While connectionist structures using weighted links do provide a functionality consistent with the physiology and psychology of cognition, conceptual graphs can incorporate both explicit data and weights.
The appeal of conceptually structured semantic networks is that they can easily be adapted to connectionist principles of weighted links. In addition to possessing labels, the links can be given adjustable weights. On the representational level, such graphs are fairly easy to implement; adjusting weights of links between explicit permanently stored data is a little harder.
If you look inside MIPUS‘s brain, you will find a lot of silicon (not implants) on chips that look squared (we still use circles to show how they are organized). This illustration shows a neural model of an associationist structure similar to MIPUS’s cognitive apparatus.
Semantic Dimensions
Semantic networks come in a variety of representation schemata, as shown at right. Most of them are graphs or trees in which relations are represented either by position in the tree or by specifically labeled arcs or edges connecting nodes that represent data objects. In type hierarchies, the relative position of nodes is often enough to represent the relation because “parent, child and sibling” constitutes an exhaustive set of the salient relations. Some type hierarchies require more expressiveness than a directed tree can provide; multiple inheritance paths are one such example. In such cases, type lattices are often preferred. In addition to hierarchical relations, semantic networks can express causal and ascriptive relations as well as other types of relations that do not involve inheritance.
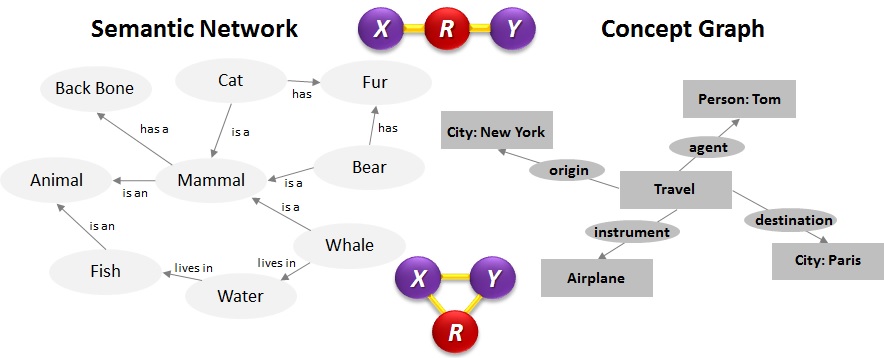
The standard model of semantic networks lends itself to flat or two-dimensional representations. That is, one entity will presumably be activated, and it will activate both a relation and another entity. Individual links in such a model for spreading activation may be graphically represented as a linear connection of two objects (X and Y) connected by a named relation (R) that controls the connection, or as a triangle in which one may assume the objects are linked directly and the named relation shares in the association. A type lattice is an example of a hierarchical semantic network that demonstrates the mathematical soundness of this type of a model.
Ontology triples, such as those defined in RDF and OWL, are effective implementations of this type of model. I favor this approach in my language understanding modeling, and I believe the fundamental structure of OWL ontologies is neuromorphic enough to classify it among the ranks of valid models of knowledge structure in the brain.
| Click below to look in each Understanding Context section |
|---|