18 Aug Modeling Positive and Negative Activation
Humans learn from both positive and negative experiences. The electrical flow between neurons can be positive (excitatory), propagating electrical potential flow along neural path to create further excitation and a bubbling-up effect, or negative (inhibitory) reducing or stopping the electrical potential flow along a pathway. Remember that a neural pathway is not like a long line, but like a bunch of neurons connected by branching fibers synaptic junctions across which electrical signals are passed like a bucket brigade. In this bucket brigade, we may compare positive activation to a flammable liquid like gasoline, and inhibitory activation a flame retardant like water. What heats up, in this process, is a pattern of excited neurons that catalyze a cognitive phenomenon such as recognition, classification, decision or stimulus directing muscle movement.
Whether the system we are attempting to build is a robot that moves about, or a language understanding system that resolves ambiguity, we can model both positive and negative flows to favor or disfavor a specific avenue of thought or action.
| Understanding Context Cross-Reference |
|---|
| Click on these Links to other posts and glossary/bibliography references |
|
|
 |
|
| Prior Post | Next Post |
| Determinacy in Neural Connections | |
Definitions |
References |
| Rumelhart 1986 | |
| Mountcastle 1978 | |
| Kandel 1985 Kuffler 1984 |
Positive and Negative
We’ve spent some time understanding neural networks that consist of nodes with links representing neurons linked by synapses:
| Neural Network Perception | Modeling Neural Interconnections |
| Roots of Neural Nets | Learning from Errors |
| Parallel Distributed Pattern Processing | Neural Networks |
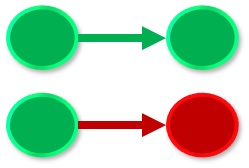For any two nodes or neurodes in an interconnected system there may be positive or negative interaction, or no interaction at all. This imitates the action of excitation and inhibition between neurons in the brain. The reason that the node on the left in the illustration at right is shown as green (implying “activated”) is that an inhibitory link cannot be triggered from a resting node, or a node that is not already excited. Nodes that are not excited are not in a pathway. During any slice of time, it is possible that most of the neurons and synaptic links in the brain are resting. We might illustrate the resting state by coloring a node blue. The links connecting nodes in a network like the one illustrated below may be weighted, such that links with higher weights may facilitate activation flow while links with lower or negative weights could impede flow.
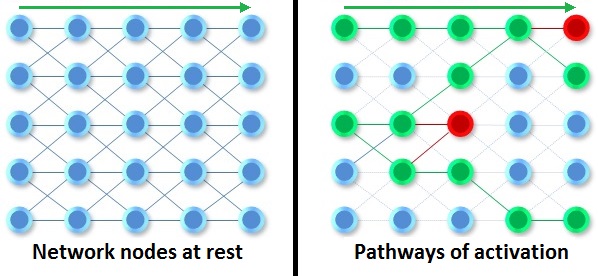
Connectionist models or PDP networks act like the illustration above with each node representing a state of “ON or “OFF” or a numerical value with a threshold representing “ON or “OFF”. These are fundamentally implicit models in which the knowledge is in the entire network, not any subsegment of it. In an explicit neural model, we could assume that each node can contain complex information, and place a constraint such as a fact, a proposition or a hypothesis at each node. We could even expand the possibilities so that a node could represent an object, an attribute or even an entire computer program.
The 3D molecular ontology model shown in the illustration at right can incorporate the following assumptions:
- the system uses multi-valued logic
- values can be positive or negative
- flow is non-directional
- weights may or may not be symmetrical
Neurons Are Not Simple
Perhaps the most important message we can derive from the evidence in Sections 1-3 of this blog is that neurons are not simple. Since they are not simple, can they be modeled using simple PEs as proposed in the connectionist model? Our contention is that we can achieve greater functionality and more neuromorphic properties with a gnostic model: a model in which all the information is stored explicitly. Here is a quick review of the data in Sections 1-3 that support such an assumption.
- the brain has many areas performing specialized tasks;
- the areas are tightly interconnected and mutually supporting;
- as neurons are not simple, their cybernetic roles may not be simple;
- neurons do not all behave the same or perform the same tasks;
- connections between neurons are neither random nor static;
- the flow of action potential between neurons is complex in intensity, duration, impact, and possibly in intracellular pathways; and
- cytoskeletal members can transduce electrical potential and may be able to adopt states that affect their transductance properties.
Complex Representations
The creation of complex internal representations suggested earlier is the most difficult aspect of migrating from a purely connectionist model to a neural model in which symbol manipulation tasks can be accomplished. One of the reasons for this difficulty is the number of different types of constraints that apply to the categories of data required for complex cognitive functions. For visual pattern recognition, the constraints that apply are shape, color, depth, relative size, and motion.
Most ANS for image recognition and classification deal with simple shapes. Some are capable of processing color. Visual processing of depth has been addressed in several models, but no systems I know of can reliably sort out the layers of objects in a picture. Where the objects in a scene represented on a two-dimensional image are located at different depths, knowledge of the relative size of the objects may be the most useful knowledge in calculating depth. That sort of symbolic knowledge must be encoded in a complex representation to be useful.
Complex representations are usually not supported by implicit models (such as the PDP model), leaving us with many new questions. Does the brain use multiple encoding schema, including both implicit and explicit? If complex representations are used to support a processing scheme composed of simple connectionist processing elements, which part is more brain-like? If both parts are physiologically consistent, how are they to be integrated into the processing scheme(ata)?
These model questions are very unsettling, and the limited results of language understanding systems have borne out the complexity of the problem. They suggest a need for a new theory that will account for the complexities of abstract cognitive phenomena. Can we do this in a neuromorphic model without building systems with billions of processors? I think we can using ontologies in conjunction with high-performance fuzzy logic.
| Click below to look in each Understanding Context section |
|---|
SHARE THIS ARTICLE
